Clustered Hashing: Incremental Resizing
Previous post doesn’t touch resize of the hash table. Usually resize of the hash table is straight-forward. A new table is created; Insert all items in the orginal table to the new table; And finally destroy the old table.
This is an expensive O(N) operation compared to lookup, insert and remove. Is there a faster way than O(n)? There is not. However, the O(N) operation in the middle of O(1) operations causes system hiccups. For a normal application, this is acceptable. There are some realtime systems where near-constant operating time is important. In these systems constant inflow of data can only be buffered for so long or buffer overrun and data loss may happen.
For this reason, an incremental resizing mechanism is designed to only move a small chunk of items from old table to new table on every insert. There are a few potential issues with this mechanism
- Uses double amount of memory during transition period.
- Lookup performance is detrimented. Lookup needs to decide which table to operate on. Or it has to look up in 2 tables.
- When the table is big, the transitory period is not so transitory anymore, especially when the move from old to new depends on insert and after resizing insertion becomes less frequent. In some cases transition may stay forever.
Trigger resize
The hash table only increase in size, it doesn’t implement shrinking in size. In real-time systems, this is a standard practice. The largest hash table usually represents the peak load of some sort which may be hit again in the future. Even if the peak is over, we leave the size for the next peak.
SizeUp is triggered by:
- threshold on insert
- 100% for table_size <= 2^3 (internal_table_size = 11)
- 75% for larger tables.
- -the table can’t hold the new item or old item as a result of relocation, ie., the overflow area overflows.
The advantage of the Clusterec Hashing is its load factor. It can have really high load factors with little sacrifice of speed. 75% is tested with normally single digit max distances from the cluster’s bucket to its tail. And this is one of the keys Clustered Hashing saves memory compared to Chained Hashing.
#define DICT_THRESHOLD_BITS 3
#define DICT_LOAD_FACTORE_BITS 2
int ThresholdEntries() const
{
int capacity = Capacity();
if( log2_buckets <= DICT_THRESHOLD_BITS)
return capacity;
return capacity - (capacity>>DICT_LOAD_FACTOR_BITS);
}
At the end of Insert(key), we add threshold test to trigger Size(). After possible size up, we continue Remap() procedure if necessary.
void Insert(Key& key, Value& value){
hash_t hash = Hash(key);
int insert_position = 0;
int insert_distance = 0;
int position = LookupIndex(key, hash, &insert_position, &insert_distance);
if( position > 0 )
{
table[i].value = value;
return;
}
Entry entry(key, value, hash, insert_distance);
InsertRelocateAndAdjust(entry, insert_position);
if( ++num_entries > ThresholdEntries() )
SizeUp();
if( Remapping() )
Remap();
}
SizeUp() triggered by the condition where the table cannot hold the item even if overall it still has space.
void InsertAndRelocate(Entry& entry, int position, int* last_affected_position)
{
while(true)
{
if(insert_position >= Capacity())
{
SizeUp();
table[insert_position] = entry;
if(last_affected_position)
*last_affected_position = insert_position;
return;
}
if(table[insert_position].Empty())
{
table[insert_position] = entry;
if(last_affected_position)
*last_affected_position = insert_position;
return;
}
auto t = table[insert_position];
int next = EndOfClusterByPosition(insert_position);
t.distance += next - insert_position;
table[insert_position] = entry;
entry = t;
insert_position = next;
}
}
In-place Resize
The no-pointer property of open table gives Cluster Hashing a really neat way to size up: It can actually size up in place. Because it doesn’t require readjustment of pointers, it can reallocate larger size with the existing table as first part of the table. We can easily achieve this with realloc() C function call. If the table has some free memory after it, it simply extends the memory space. If it doesn’t, relalloc() allocates a larger memory and copy the existing table to the new memory as the first part. This should be a very fast operation.
Remapping() condition is setup when remap_end is set to a value equal or greater than zero.
remap_end is set to prev_capacity instead of prev_capacity - 1 to accomodate SizeUp() triggered inside InsertAndRelocate() where the new item is put to [prev_capacity] after SizeUp().
remap tracks how many unfinished remapping is going on including the current one. This is used for lookup in a mixed hash table discussed in lookup sections.
void SizeUp()
{
int prev_capacity = Capacity();
log2_buckets++;
int capacity = Capacity();
table = (DictEntry*)realloc(table, capacity*sizeof(DictEntry));
for(int i=prev_capacity; i<capacity; i++)
table[i].SetEmpty();
remap_end = prev_capacity;
...
}
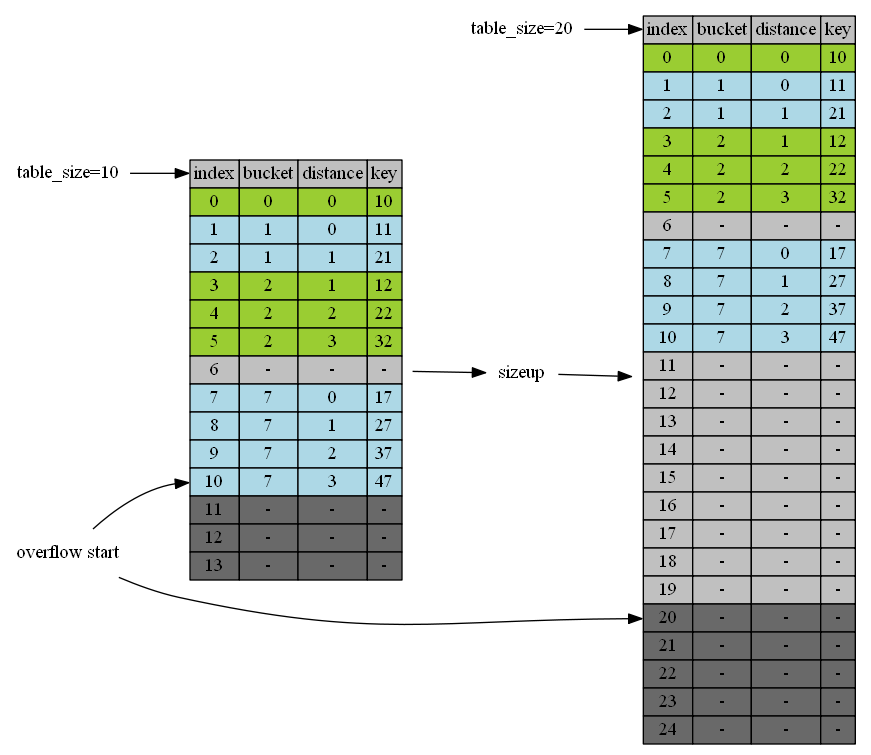
Remap
After table sizes up, all items become old and need to be relocated to positions based on new table_size. remap_end is set to the previous size of the table. It splits table into two ranges: [0,remap_end] and (remap_end, capacity). remap_end, right after SizeUp, is set to capacity of previous table on purpose to accomodate the newly inserted item in InsertAndRelocate() right after SizeUp(). New items are inserted into [0, remap_end] or (remap_end, capacity), but old items remain in [0, remap_end]. After sizeup and some inserts, we know that range [0,map_end] is mixed with items mapping to previous table sizes and current table size. and (map_end, capacity) contains only correctly mapped items.
For old items in the mixed range [0, remap_end] we need to remove them from the table and insert back again to fix its bucket in the table with new size. This process is called remapping. We remap the items from bottom of the remap range until the top. As incremental resizing indicates, we remap a small set of items for every new inserts.
Remap range [0,remap_end] usually shrinks after each remap. However, Remap may also cause the range to grow if inserting part of remapping pushes an old item from ummapped range to mapped range. We detect this case at the end of InsertRelocateAndAdjust(). If remap_end is in the range of [insert_position, last_affected_position], we know that possibly one item was in the unmapped range but now crossees remap_end to the map;ped range. We expand unmapped range to cover this case.
void InsertRelocateAndAdjust(Entry& entry, int insert_position)
{
int last_affected_position = position;
InsertAndRelocate(entry, insert_position, &last_affected_position);
if( Remapping() && insert_position <= remap_end && remap_end < last_affected_position )
remap_end = last_affected_position;
...
}
Because remap_end may change while we call Remap(position), we don’t decrease remap_end by one after each Remap(position). Instead, we decrease it only if Remap(position) returns false. That is, only when we are sure that remap_end is already mapped and doesn’t need to remap again.
void Remap()
{
int left = DICT_REMAP_ENTRIES; //max entries to remap at a time.
while(remap_end >= 0 && left > 0)
{
if(!table.Empty(remap_end) && Remap(remap_end))
left--;
else
remap_end--;
}
...
}
How do we know if an item is an old item or not? We don’t have to know. For each item of key K, we recalculates its bucket based on new table size: bucket=M(H(K),table_size) and based on its position we can calculate its current bucket: bucket=position-distance. If two buckets are the same, we don’t have to remap it. This is the same for all new items and some old items.
With the table size of 2^N and fibonaci hashing, only half of the old items need to be remapped. Here is how it works:
bucket = M(hash, N) = lower N bits of (hash * constant)
when N increase by 1, N+1, lower N=1 bits of (hash * constant)` is the bucket. It simply added one more higher bit to the bucket. The new bit could be 0 or 1. When it’s 0, it’s bucket is the same of the previous one. Only when the new bit is 1 the bucket doubles.
This is a big boost in performance compared to other incremental resizing mechanisms.
bool Remap(int position, int* new_position)
{
int current = BucketByPosition(position);//current bucket
int expected = BucketByHash(table[position].hash, log2_buckets);
if( current == expected )
return false;
Entry entry = RemoveAndRelocate(position);
int insert_position = EndOfClusterByBucket(expected);
if( new_position )
*new_position = insert_position;
entry.distance = insert_position - expected;
InsertAndRelocate(entry, insert_position);
return true;
}
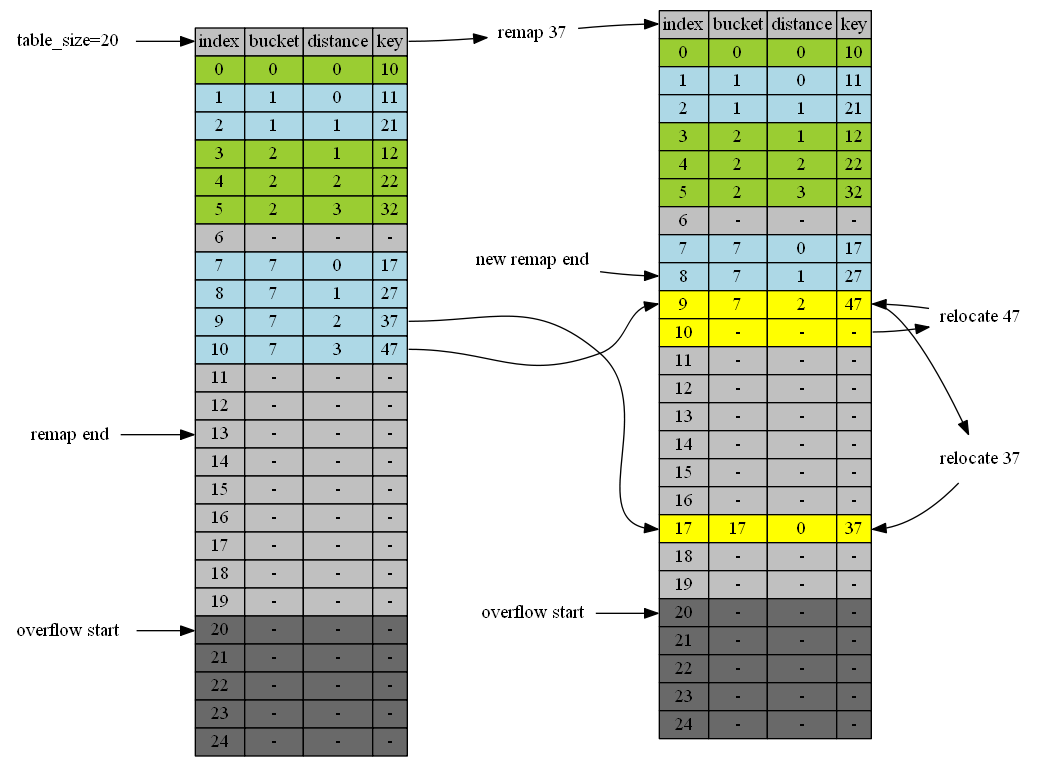
In the diagram below, left table shows the state right after the size up. dark grey area is the overflow area. remap_end is set the the last position before table resizes. The old table_size = 10, the new one is 20. During first remapping, we go from bottom (13) up. Position 13,12,11 are empty. No adjustment. Position 10 is 47. new bucket is 47%20=7, the same as before. No change. Position 0 is 37. bucket = 37 % 20 = 17. new bucket is 17 while current bucket is 7. So take 47 out by calling remove(9). Removal of 9 causes position 10 to shift up. So 47 is relocated to position 9. insert(37) put item 37 to bucket 17.
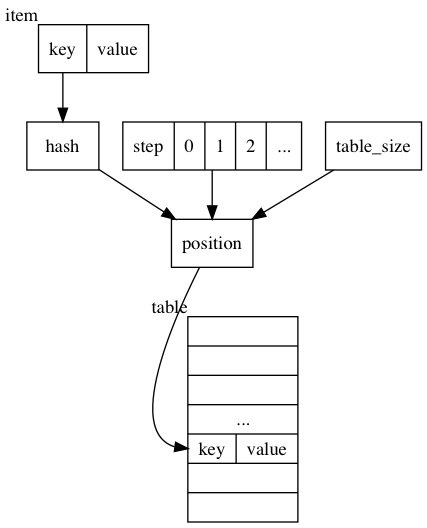
Lookup
After resize, the new table is divided into two ranges: mixed range [0, remap_end] that contains mixed items and mapped range (remap_end, capacity). A normal lookup in post Clustered Hashing: Basic Operations will find all items whose bucket is mapped to new table size. Thses items include new ones inserted after the table resize, old items remapped based on new table sizes, and some old items whose bucket calculated based on old table sizes is the same as the one calculated in new table size.
If we cannot find the item according to normal lookup, that means either it doesn’t exist, or it’s an old item in the mixed range [0,remap_end] and its bucket is different if calculated from new table size. To find them, we need to calculate all possible buckets according to all previous table sizes(S0, S-1, S-2, …).
Post Clustered Hashing explains the rehash/remap mechanism. A step parameter is applied during mapping from hash to bucket. In clustered Hashing table the distance from its bucket is actually the step.
By looking through all previous table sizes, we expand the mapping function as shown below:
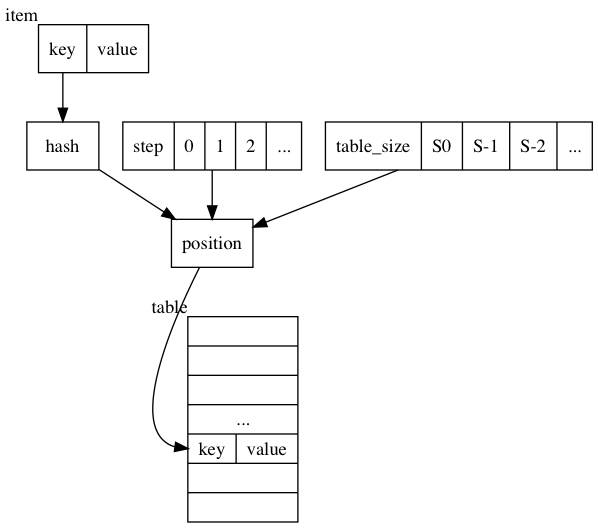
If every time we resize, we keep the table size in a queue. When we can’t find the item the normal way, and the unmapped range is not empty, we can go through the queue and try all of them out. In fact, we don’t have to go through all previous table sizes. We know that mix of items only happens during remapping process (to map old items to new table sizes). If we track how many pending remaps in progress, we only need to track back that far from end of table size queue to determine if the item is in the table or not. We maintain remaps counter for this. Each resize we increase it by one. When remapping procedure finishes, we reset it to zero.
void SizeUp()
{
int prev_capacity = Capacity();
log2_buckets++;
int capacity = Capacity();
table = (DictEntry*)realloc(table, capacity*sizeof(DictEntry));
for(int i=prev_capacity; i<capacity; i++)
table[i].SetEmpty();
remap_end = prev_capacity;
remaps++;
}
void Remap()
{
int left = DICT_REMAP_ENTRIES; //max entries to remap at a time.
while(remap_end >= 0 && left > 0)
{
if(!table.Empty(remap_end) && Remap(remap_end))
left--;
else
remap_end--;
}
if( remap_end < 0 )
remaps = 0;
}
If we only grow the table, We don’t even need to maintain the table size queue. As table size roughly doubles every time, we can infer all previous table sizes based on the current table size.
The expaned wrapper function for LookupIndex() is below: If normal lookup doesn’t find the item, we go through previous table sizes up to remaps times. And we only need to find it in [0,remap_end] range because if it’s in (remap_end, capacity) range, it should be found in the normal lookup. When item is not found, we need to keep the insert_position and insert_distance during normal lookup, because we insert into the table according to current table size instead of previous ones.
int LookupIndex(Key key, hash_t hash, int* insert_position = NULL, int* insert_distance = NULL)
{
if( !table )
return -1;
int bucket = BucketByHash(hash);
int end = Capacity();
int position = LookupIndex(key, hash, bucket, end, insert_position, insert_distance);
if( position >= 0)
return position;
for(int i=1; i<=remaps; i++)
{
int prev_bucket = BucketByHash(hash,log2_buckets - i);
if( prev_bucket <= remap_end)
{
position = LookupIndex(key, key_size, hash, prev_bucket, remap_end+1);
if(position >= 0)
{
Remap(position, &position);
return position;
}
}
}
return -1;
}
From simple Open Addressing Hashing to Clustered Hashing, we’ve broken a few rules to boot the performance:
- insert can modify existing item’s positions
- remove can modify existing item’s positions
- look can modify existing item’s positions.
Here’s the optimized algorithm: When we successfully looked up an item successfully in more than one tries, we remap the item to a new positions according to current table size. It sacrifices a bit of time on the first lookup to make the sequential lookups on the same item faster. This is also a good complement to remap when inserting new items. If inserting new items becomes less frequent but lookup becomes more frequent, this improvement make a big difference.
The next post touches a special requirement on some hash tables: Clustered Hashing: Modify On Iteration