Clustered Hashing: Modify On Iteration

Iteration on the hash table is usually a constant operation. It doesn’t modify the table. Since it’s constant, the implementation is straight-forward. It’s even simpler for open addressing hash tables: just go through every index of the table, skip empty items.

Some rare scenarios require hash tables to be able to modify itself while in iteration. For example, in a hash table of integers, you want to insert a even number for every odd number.

With a constant iteration, you iterate all the keys. For each odd key that an even key is to be inserted, you insert it to an external container such as vector. Then you go through the vector and insert them all to the hash table.

    map<int,int> mp;
    vector<pair<int,int>> v;
    for( auto& [k,v]: mp)
    {
        if(k%2)
            v.push_back(make_pair(k+1,k+1));
    }
    for( auto i: v)
    {
        mp[i.first] = i.second;
    }

However, this is only good for a one-pass operation. If the condition is set so that the newly inserted item may also qualify, a more complex algorithm is needed aside hash table. Allowing insert on iteration can solve this problem without help of another container.

    map<int,int> mp;
    for( auto& [k,v]: mp)
    {
        if(k%2)
            mp[k+1] = k+1;
    }

The project I worked on (zeek.org) requires support of modification on iteration. Below is how it is implemented on Clustered Hashing.

Basic Idea

For each iteration, we maintain an iteration cookie to keep state of the iteration. The hash table keeps a list of iteration cookies for adjustment on modification.

Iteration Cookie uses next non-empty item to output. It also maintains inserted list for items inserted before next during iteration. Similarly, it uses visited to keep items that was before next but now after next due to relocations of items on insert or remove during iteration. next splits hash table items into 2 ranges: iterated range [0,next) and to-be-iterated range [next, capacity).

struct IterCookie
{
    int next;
    vector<Dictionary::Entry> inserted;
    vector<Dictionoary::visited;
};

class Dictionary
{
    ...
    vector<IterCookie*> cookies;
};

Iteration

Iteration on open addressing hash table is straight-forward. Goes through every item in the table, skipping empty positions. With inserted and visited, we iterate inserted first. For each item in the table, we ignore if it’s in the visited list. At the same time, remove the item from visited because it’s already iterated and the item is unique in the hash table to keep visited as short as possible.

///given position, find the next non-empty item. pass -1 to get the first one. return Capacity() if no more.
int Next(int position)
{
    do
    {
        position++;
    } while( position < Capacity() && table[position].Empty());
    return position;
}

bool NextEntry(Key& key, Value& value, IterCookie& it)
{
    //iterate inserted first.
    if(!it.inserted.empty())
    {
        Value v = it.inserted.back().value;
        k = it.inserted.back().key;
        it.inserted.pop_back();
        return v;
    }

    if( it.next < 0 ) //initial value.
        it.next = Next(-1);

    if( it.next >= Capacity() )
        return false;

    //special case in sizeup during iteration.
    if( table[it.next].Empty() )
        it.next = Next(it.next);

    //ignore items in visited.
    while( it.next < Capacity() )
    {
        ASSERT(!table[it.next].Empty());
        auto entry = find(it.visited.begin(), it.visited.end(), table[it.next]);
        if( entry == it.visited.end())
            break;
        it.visited.erase(it);
        it.next = Next(it.next);
    }

    if( it.next >= Capacity() )
        return false;

    key = table[it.next].key;
    value = table[it.next].value;
    it.next = Next(it.next);
    return true;
}

Adjustment on insert during iteration

Adjustment on insert is to manipulate inserted and visited list. If an item is inserted but passed the next iteration point, it’s added to inserted list to be iterated. If an item was iterated but now pushed down passing next iteration point, we put it into visited list for it to be ignored.

Inserting a new item into position p affects the range [p,q], where p is the insertion position of the item. q is the last_affected_position according the the algorithm of insert in post Clustered Hashing: Basic Operations. The new item is inserted into p and items within [p+1,q] are adjusted.

An iteration is in progress, with its next to be iterated the next round.

handle newly inserted item at [p]

An item inserted before next will not be iterated normally because iterator will not go back. In this case, we put it into inserted list.

void InsertRelocateAndAdjust(Entry& entry, int insert_position)
{
    int last_affected_position = position;
    InsertAndRelocate(entry, insert_position, &last_affected_position);
    if( Remapping() && insert_position <= remap_end && remap_end < last_affected_position )
        remap_end = last_affected_position;
    for( auto c: cookies)
        AdjustOnInsert(c, entry, insert_position, last_affected_position)
}

void AdjustOnInsert(IterCookie& c, Entry& entry, int insert_position, int last_affected_position)
{
    if( insert_position < c.next )
        c.inserted.push_back(entry);
    ...
}

handle adjustment of items

Detect adjustment range where if next is in, the adjustment is necessary

The new item is inserted to [p]. The first item that moves from is [p]. The last position an item moves to is [q].

• if next<=p, no item’s before next, so no item can cross down next.
• if next>q, no item’s at or after next, so no item can cross to at or after next.

This means the range where adjustment is necessary, ie. adjustment range, is [p+1,q].

The following diagram shows the conditions when next is out of adjustment range [p+1,q].

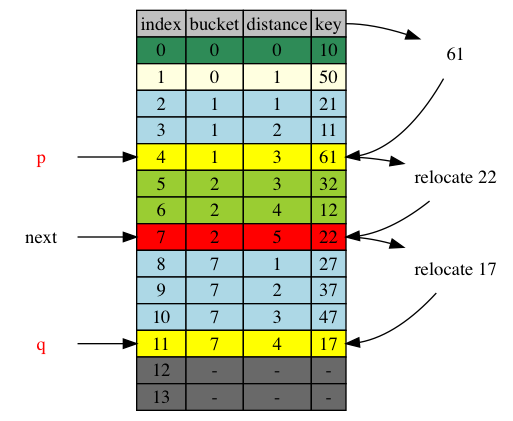
In the following hash table, we insert item 61. It’s bucket b = 1. According to insert algorithm, it’s appened to the tail of the cluster 1. Its insert position p = 4. [p+1,q] = [5,11] is the adjustment range where item 22 has been moved from position 4 to position 7 and item 17 has been moved from position 7 to 11.

next = 3. The adjustment happens in the to-be-iterated range for iterator. No adjustment is necessary.

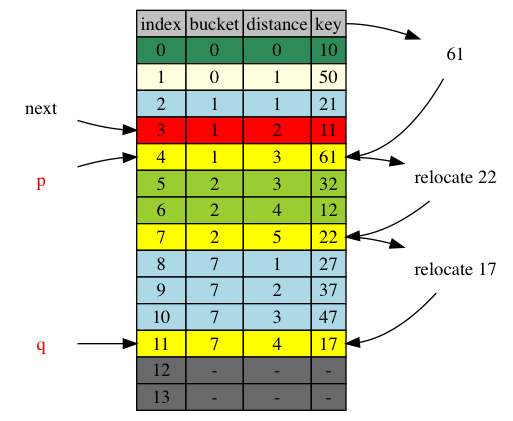
next = 4, right on the insert_position p. Newly inserted item at p is handled by inserting it to inserted container. The first adjustment element, 22, was in position 4, which is at next, within to-be-iterated range [p+1,]. It is yet to be iterated. It’s new posision, position 7, is also in the to-be-iterated range. No adjustment is necessary.

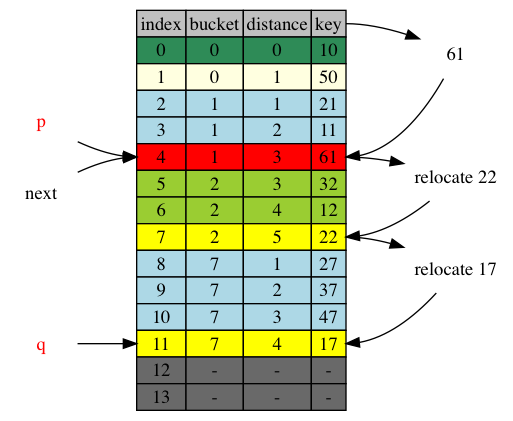
next = 12, right after the adjustment range [p+1,q], ie. [5,11]. The adjusted items, 22 and 17, has been iterated already. They are still in the iterated range [,12). No adjustment is necessary.

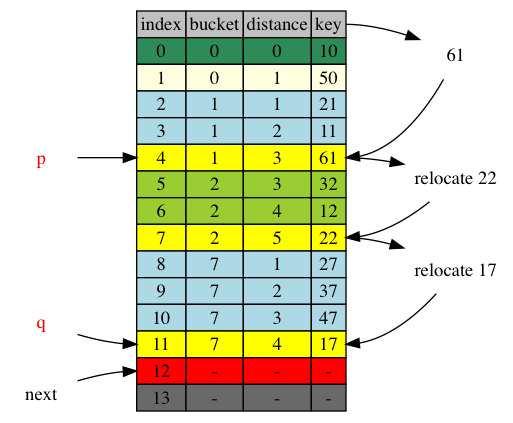
To sum up, if next is out of adjustment range [p+1,q], no adjustment is necessary.

when next is within adjustment range [p+1,q]

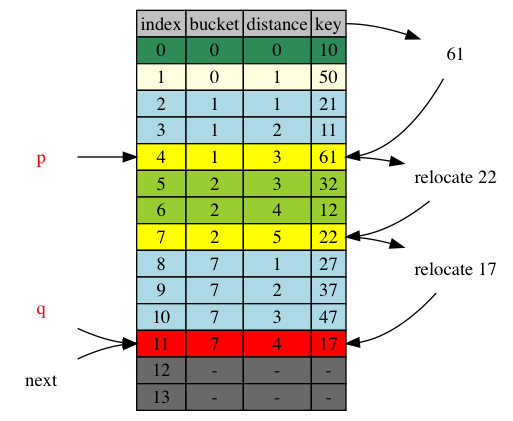
Things are getting interesting within the range. Let’s see an example when next = 5 From the chart, we can spot visually that item 22 is the only item (was in position 4) that was in iterated range [0,5), and is now at position 7, in the to-be-iterated range [5,]. In this case, we put item 22 to visited.

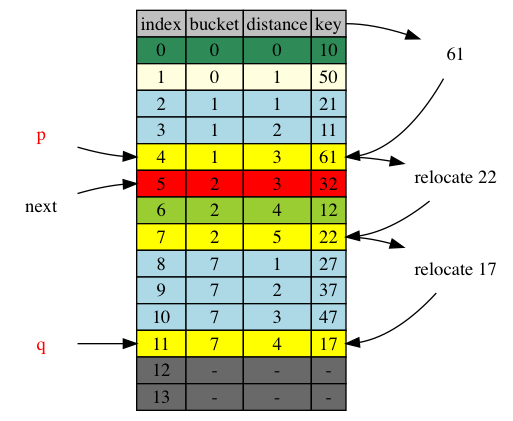
Our first question is: how many items may cross the next boundary? The answer is one and only one. Here is the proof.

From the right of the diagram we see the relocating paths. Based on the insertion adjustment algorithm,

• The complete path covers the whole adjustment range.
• Individual relocating arcs don’t overlap with each other. They are simply connected. The end of one arc becomes the start of the next arc.

If we draw the line of next horizontally, it will cross one and only one arc. As each arc represents one relocation, we know that one and only one relocation cross next boundary.

Given that one and only one item crosses the boundary, our second question is what is this item?

According to the insert algorithm, when we adjust an item, we take it out and append it to the tail of its cluster. So the crossed item is the tail of its cluster. But which cluster? We know the crossed item move from its head and to its tail and it crosses next position. This means next also belongs to its cluster after the adjustment. So it’s the cluster next is in. crossed_item = TailOfClusterByPosition(next)

The complete AdjustOnInsert function becomes

void AdjustOnInsert(IterCookie& it, Entry& entry, int insert_position, int last_affected_position)
{
    if (insert_position < c->next)
        c.inserted.push_back(entry);

    if (insert_position < it->next && it->next <= last_affected_position)
    {
        int k = TailOfClusterByPosition(it.next);
        it.visited.push_back(table[k]);
    }
}

next = 7. table[next] itself is the tail of its cluster. item 22 crossed.

next = 11. table[next] itself is the tail of its cluster. It’s also the end of the adjusted range. Item 17 has crossed.

Adjustment on remove during iteration

Removing item on position p makes [p] an empty position. This empty space triggers adjustments of the items following position p, by moving some items up to improve their distances. q is either the end of table, capacity, or [q] is empty.

Handle removed item

The removed item could be recently inserted into inserted list. So it’s necessary to remove it from inserted.

Remove adjustment is added to RemoveRelocateAndAdjust(int position) function

Entry RemoveRelocateAndAdjust(int position)
{
    int last_affected_position = position;
    Entry e = RemoveAndRelocate(position, &last_affected_position);
    for( auto c: cookies)
        AdjustOnRemove(c, e, position, last_affected_position);
    return e;
}

handle the removed item

If item is removed before the next iteration position, it’s alrerady iterated and we cannot undo it. If the item is removed at or after next in hash table, it will not be iterated naturally. However, we need to remove the item from inserted container if it’s there.

void AdjustOnRemove(IterCookie& c, Entry& entry, int position, int& last_adjusted_position)
{
    c.inserted.erase(remove(c.inserted.begin(), c.inserted.end(), entry), c.inserted.end());
    ...
}

Detect adjustment range

The modified range is [p,q].

• if next <= p, no item moves up before next as the last item moved to is at [p].
• if next > q, no item moves from at or after next

So the adjustment range is [p+1,q]

The following diagrams illustrates next out of adjustment range [p+1,q].

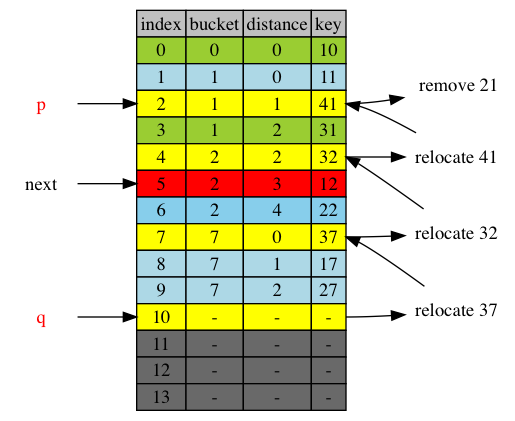
Here is the original table before removing 21.

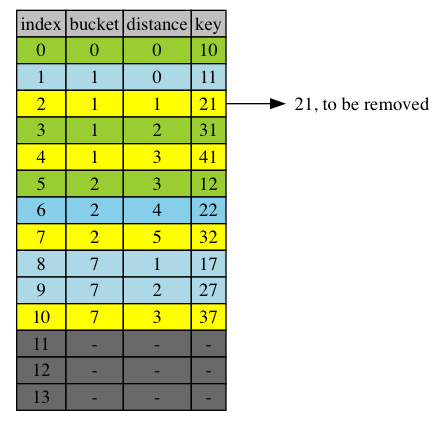
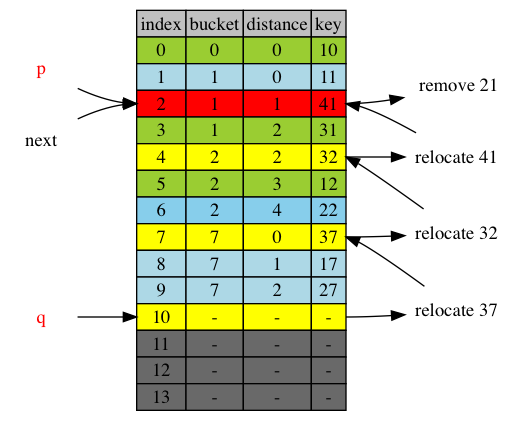
The following diagram shows removing 21 from the table. Item 21’s bucket = 1. It was at position 2, with distance of 1 to its bucket. Removing 21 causes relocation of 41, tail of its cluaster from position 4 to position 2 to fill the new vacancy. Then item 32, tail of cluster 2, at position 7, relocated to position 4, to become head of cluster 2. Similarly, item 37 is relocated from 10, tail of cluster 7 to position 7, now head of the cluster 7.

next = p = 2

Crossing of next up is defined as that the item was at or after next, and relocated before next. Although position 2, next is removed and refilled, no items moved before position 2. So no adjustment is necessary.

The next 2 diagrams show when next is around the end of the range. As we can see, there’s no element that’s relocated at or after next. Not crossing is possible. No adjustment is necessary.

next = q = 10

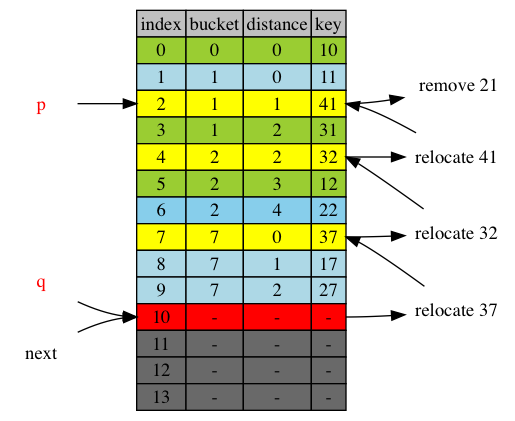
next = q+1 = 11

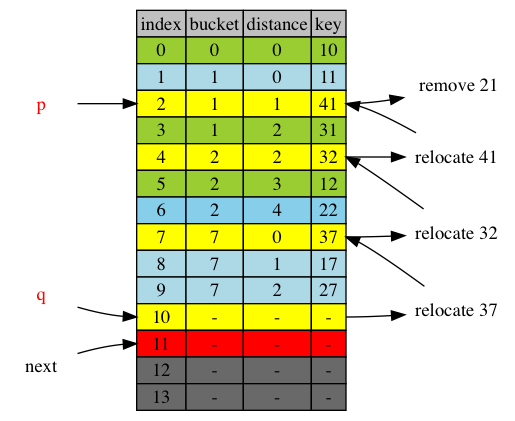
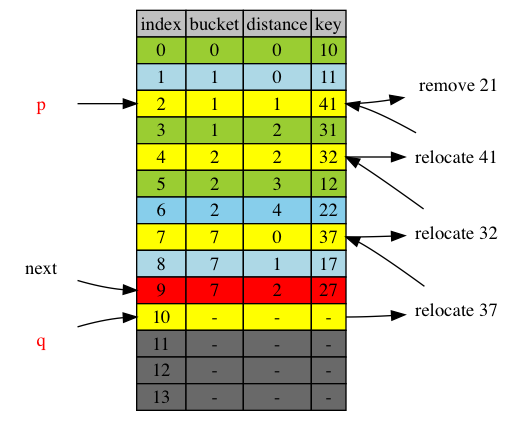
when next is within adjustment range [p+1,q]

Relocation path in removal is similar to insert with opposite direction. Relocation path covers the whole adjustment range. It’s composed by relocating arc connected continuously one after the other without overlap, as illustrated below.

next = p+1 = 3

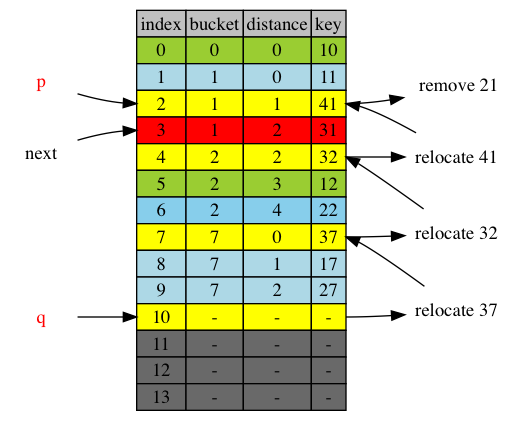
There is one and only one item that crosses up next boundary. It was at or after next before relocation and is before next after relocation.

In the diagram item 41 is the item that crosses next=3, from position 4 to position 2. How do we find this item?

• The item is now before next
• The item belongs to the cluster immediately before next
• The item is the head of its cluster unless it’s the item that fills the first vacancy, position p.

The item is the head of the cluster right befor next, but cannot be smaller than p. So the item is at the position max(position,HeadOfClusterByPosition(next-1)) because next is in range [p+1,q], next-1 is always valid.

Because remove leave one empty position, it this position happens to be next, then we need to adjust next to the next valid item or end of table.

void AdjustOnRemove(IterCookie* c, const Entry& entry, int position, int last_adjusted_position)
{
    c->inserted.erase(remove(c->inserted.begin(), c->inserted.end(), entry), c->inserted.end());
    if (position < c->next && c->next <= last_adjusted_position)
    {
        int moved = HeadOfClusterByPosition(c->next-1);
        if( moved < position )
            moved = position; 
        c->inserted->push_back(table[moved]);
    }
    if(c->next < Capacity() && table[c->next].Empty())
        c->next = Next(c->next);
}

Following the rules above, on diagram above, we have:

• p=2, q=10
• next==3
• next-1=2
• HeadofClusterByPosition(2) = 1
• max(p,1) = max(2,1)=2, ie. position p.

More examples below:

next = 4, head of cluster at position 3 is position 1, smaller than p, so the crossed item is at p instead. p=2, it’s 41. 41 crosses from position 4 go position 2.

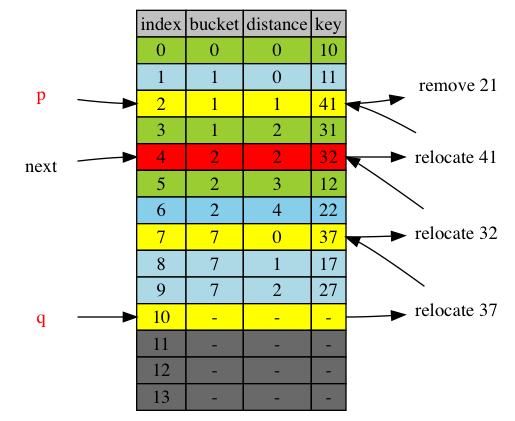
next = 5, head of cluster at next-1, position 4, is position 4. So it’s item 32 at position 4 after relocation.

next = 9, head of cluster at next-1, position 8, is position 7. So it’s item 37 at position 7 after relocation.

More on iterations

Adjusting iteration cookies during insert and remove is expensive. When iteration is in progress, we adapt certain operations.

lookup on iteration

Avoid lookup optimization by moving not-in-place items to its right position after sizeup.

Remap on iteration

Avoid Remap when iteration is in progress.

References

• Clustered Hashing
• Clustered Hashing: Basic Operations
• Clustered Hashing: Incremental Resize
• Clustered Hashing: Modify On Iteration
• Sebastian Sylvan, Robin Hood Hashing should be your default Hash Table implementation
• Malte Skarupke, Fibonacci Hashing: The Optimization that the World Forgot